By Long Luo

众所周知，计算机系统从 \(16\) 位发展到 \(32\) 位，再从 \(32\) 位发展到 \(64\) 位，与此同时不同的数据类型也随着系统的位数增大而增大。早期的操作系统是 \(16\) 位系统，int用2字节表示，范围是-32768~32767，long用4字节表示，范围是-2147483648~2147483647；后来发展到 \(32\) 位操作系统，int用4字节表示，与long相同。

目前的操作系统已发展到 \(64\) 位操作系统，但因程序编译工艺的不同，两者表现出不同的差别：

• \(32\) 位编译系统：int占四字节，与long相同。
• \(64\) 位编译系统：int占四字节，long占8字节，long数据范围变为：\(-2^63~2^63-1\)

具体在标准中，并没有规定long一定要比int长，也没有规定short要比int短，只是规定了长整型至少和整型一样长，整型至少和短整型一样长。这个规则同样适用于浮点型long double至少和double一样长，double至少和float一样长。至于如何实现要看编译器厂商。

下表所展示的是Java的8种基本数据类型的详细数据：

从上述表格中可以看出，普通工作生活中所涉及的数字都不会超过int所能表示的范围，而超过long long类型则少之又少。但是具体到一些行业或者科研中，比如天文，石油开采等，经常需要和天文数字进行打交道。举例来说，\(50!\)，\(10^20\) 这种阶乘或者指数函数轻而易举就突破最大所能表示的范围。

如何表示这些超大数字以及对其进行数学运算呢？

大数字如何表示？

首先需要解决的问题就是如何表示，用数据类型是不可能了，那么我们应该怎么做呢？

很容易想到的就是将超大数字拆分为一个个位进行展示，存储这些位的值就可以了。至于怎么存，可以使用string, 也可以使用list, array等。这里为了方便，我们使用string来说明及展示。 例子：

1

string number = "3377733333332222";

解决了展示问题，下面我们来展示如何对超大数字进行数学运算：

加法(Add)

让我们回到小学课堂，重温我们学习加法的第一课。回想我们是如何做加法的呢？

1
2
3

Input  : str1 = "3333311111111111", 
		 str2 =   "44422222221111"
Output :         3377733333332222

很明显，我们是从低位开始，按位相加，直至最高位。

那么实现大数字的加法就可以很简单的分成3步： 1. 翻转每个string； 2. 从第 \(0\) 位开始依次相加到相对小的string，每位的数字是 \(sum mod 10\) ，如果有进位则进位为 \(sum / 10\)； 3. 对得到的结果进行翻转。

我们直接看实现吧：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

string sum_of_large_number(string num1, string num2) {
    if (num1.length() > num2.length()) {
        swap(num1, num2);
    }

    int len1 = num1.length();
    int len2 = num2.length();
    reverse(num1.begin(), num1.end());
    reverse(num2.begin(), num2.end());

    string result = "";
    int carry = 0;
    for (int i = 0; i < len1; i++) {
        int sum = (num1.at(i) - '0') + (num2.at(i) - '0') + carry;
        result.push_back(sum % 10 + '0');
        carry = sum / 10;
    }

    for (int i = len1; i < len2; i++) {
        int sum = num2.at(i) - '0' + carry;
        result.push_back(sum % 10 + '0');
        carry = sum / 10;
    }

    if (carry) {
        result.push_back(carry + '0');
    }

    reverse(result.begin(), result.end());
    return result;
}

By Long Luo

Do you remember the first time going to somewhere that you enjoyed a lot? Well I remember my first time at Chimelong Ocean Kingdom . To be honest this was my first time going to Chimelong Resort. I know what you’re probably thinking right now “wow! He hasn’t been to the before!”.

As part of our annual company team-building activity, we embarked on a day journey to Chimelong Ocean Kingdom in Zhuhai. This extraordinary adventure park is known to house one of the world’s largest aquariums, making it a must-see attraction for marine life enthusiasts like myself.

The highlight of the aquarium was the whale shark, a magnificent creature stretching over ten meters in length. It was truly awe-inspiring to witness such a gigantic, graceful creature up close. The aquarium was also teeming with an array of other aquatic life forms, each one more fascinating than the last.

By Long Luo

find 指令是 Unix/Linux 系统中很常用的指令之一，在日常开发维护中常常使用到这个工具。find 是一个很有用的指令，它支援非常多的查找选项，可以依照权限、拥有者、群组、文件类型、日期与大小等条件来查找，这里整理了一些常用的 find 指令的使用技巧。

1. Find files by name

$ find /home/user/documents -name “example.txt”

2. Find files by extension

$ find /var/log -name “*.log”

$ find /etc -mtime -7

$ find /usr/local -mtime +30

$ find /tmp -name “oldfile.txt” -delete

$ find /var/www -empty

$ find /home/user/downloads -size +100M

$ find /home -user username

$ find /etc -perm 0644

$ find /var/log -name “*.log” -exec {} ;

$ find /home/user/documents -type f -empty -exec {} ;

$ find /home/user/documents -type f -exec {} ;

$ find / -path “/proc” -prune -o -name “*.conf -print

$ find /var/www -mmin -60

$ find /home/user/pictures -name “*.jpg” | xargs tar -czvf archive.tar.gz

$ find /usr/bin -type I

17. Find Files by Inode Number

$ find / -inum 456332

$ find /home/user -not -name “*.txt”

$ find /var/log -group syslog

$ find /home/user/downloads -size +50M -size -100M

$ find /var/log -type f -exec s {} +

$ find /var/log -mmin -120

$ find /home -user username -group groupname

$ find /var/log -perm 600

$ find /var/log -size +1G -exec {} ;

$ find /home/user -maxdepth -name “*txt”

$ find /var/log -atime +90

$ find /home/user -name “.*”

$ find /home/user -ctime +1

$ find /dev -type b

$ find / -perm /a=r -not -perm /a=w

$ find /home/user -name “config”

参考文献

1. find (Unix)
2. find (Windows)
3. findstr

By Long Luo

机器学习中需要训练大量数据，涉及大量复杂运算，例如卷积、矩阵等。这些复杂运算不仅多，而且每次计算的数据量很大，如果能针对这些运算进行优化，可以大幅提高性能。

一、矩阵乘法

假设 \(A\) 为 \(m \times p\) 的矩阵，\(B\) 为 \(p \times n\) 的矩阵，那么称 \(m \times n\) 的矩阵 \(C\) 为矩阵 \(A\) 与 \(B\) 的乘积，记作 \(C = AB\)，称为矩阵积（\(\textit{Matrix Product}\)）。

其中矩阵 \(C\) 中的第 \(i\) 行第 \(j\) 列元素可以表示为：

\[ (AB)_{ij} = \sum_{k=1}^{p}{a_{ik}b_{kj}} = a_{i1}b_{1j} + a_{i2}b_{2j} + \cdots + a_{ip}b_{pj} \]

如下图所示：

假如在矩阵 \(A\) 和矩阵 \(B\) 中，\(m=p=n=N\)，那么完成 \(C=AB\) 需要多少次乘法呢？

1. 对于每一个行向量 \(r\) ，总共有 \(N\) 行；
2. 对于每一个列向量 \(c\) ，总共有 \(N\) 列；
3. 计算它们的内积，总共有 \(N\) 次乘法计算。

综合可以看出，矩阵乘法的算法复杂度是：\(O(N^3)\)。

二、Strassen算法

那么有没有比 \(O(N^{3})\) 更快的算法呢？

1969年，Volker Strassen 提出了第一个算法时间复杂度低于 \(O(N^{3})\) 矩阵乘法算法，算法复杂度为 \(O(n^{log_{2}^{7}})=O(n^{2.807})\) 。从下图可知，\(\textit{Strassen}\) 算法只有在对于维数比较大的矩阵( \(N > 300\) ) ，性能上才有很大的优势，可以减少很多乘法计算。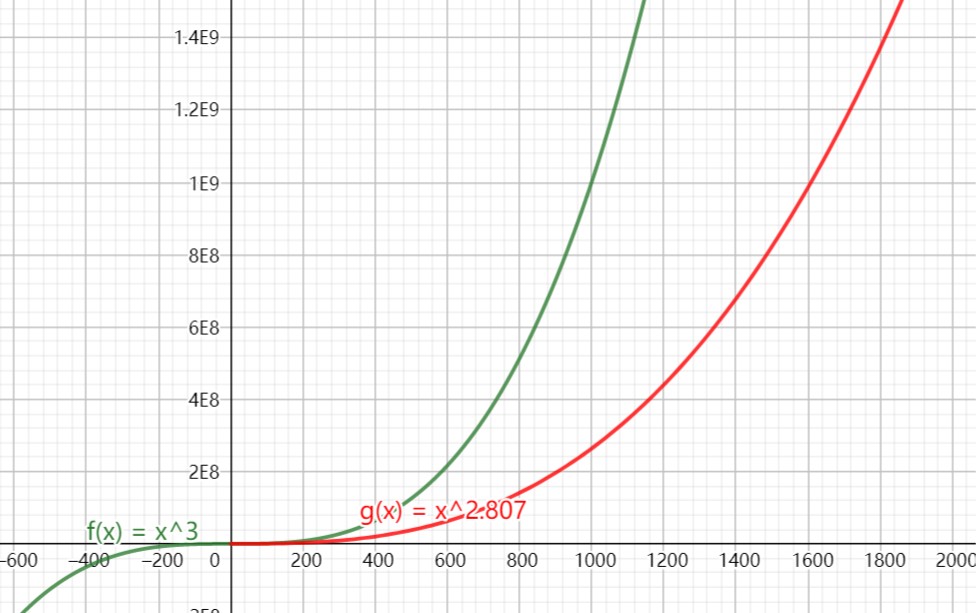

\(\textit{Strassen}\) 算法证明了矩阵乘法存在时间复杂度低于 \(O(N^{3})\) 的算法的存在，后续学者不断研究发现新的更快的算法，截止目前时间复杂度最低的矩阵乘法算法是 Coppersmith-Winograd 方法的一种扩展方法，其算法复杂度为 \(O(n^{2.375})\) 。

三、Strassen原理详解

假设矩阵 \(A\) 和矩阵 \(B\) 都是 \(N \times N (N = 2^{n})\) 的方矩阵，求 \(C = AB\) ，如下所示：

\[ \begin{aligned} A = \left [\begin{matrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{matrix} \right] \\ B = \left [\begin{matrix} B_{11} & B_{12} \\ B_{21} & B_{22} \\ \end{matrix} \right] \\ C = \left [\begin{matrix} C_{11} & C_{12} \\ C_{21} & C_{22} \\ \end{matrix} \right] \end{aligned} \]

其中

\[ \begin{bmatrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{bmatrix} = \begin{bmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{bmatrix} \cdot \begin{bmatrix} B_{11} & B_{12} \\ B_{21} & B_{22} \end{bmatrix} \]

矩阵 \(C\) 可以通过下列公式求出：

\[ \begin{aligned} C_{11} = A_{11} \cdot B_{11} + A_{12} \cdot B_{21} \\ C_{12} = A_{11} \cdot B_{12} + A_{22} \cdot B_{21} \\ C_{21} = A_{21} \cdot B_{11} + A_{22} \cdot B_{21} \\ C_{22} = A_{21} \cdot B_{12} + A_{22} \cdot B_{22} \\ \end{aligned} \]

从上述公式我们可以得出，计算 \(2\) 个 \(n \times n\) 的矩阵相乘需要 \(2\) 个 \(\frac{n}{2} \times \frac{n}{2}\) 的矩阵 \(8\) 次乘法和 \(4\) 次加法。

我们使用 \(T(n)\) 表示 \(n \times n\) 矩阵乘法的时间复杂度，那么我们可以根据上面的分解得到下面的递推公式：

\[ T(n) = 8 \times T(\frac{n}{2}) + O(n^{2}) \]

其中：

1. \(8T(\frac{n}{2})\) 表示 \(8\) 次矩阵乘法，而且相乘的矩阵规模降到了 \(\frac{n}{2}\)。
2. \(O(n^{2})\) 表示 \(4\) 次矩阵加法的时间复杂度以及合并矩阵 \(C\) 的时间复杂度。

最终可计算得到 \(T(n)=O(n^{log_{2}^{8}})=O(n^{3})\) 。

可以看出每次递归操作都需要 \(8\) 次矩阵相乘，而这正是瓶颈的来源。相比加法，矩阵乘法是非常慢的，于是我们想到能不能减少矩阵相乘的次数呢？

答案是当然可以！！！

\(\textit{Strassen}\) 算法正是从这个角度出发，实现了降低算法复杂度！

By Long Luo

Leetcode 172. 阶乘后的零 题解：

方法一：用大数暴力求解并计算末尾0的数量

因为 \(n!\) 得到的数字会非常大，所以需要使用BigInteger，得到结果之后，再计算末尾 \(0\) 的数量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

import java.math.BigInteger;

class Solution {
    public int trailingZeroes(int n) {
        BigInteger nFactorResult = BigInteger.ONE;
        for (int i = 2; i <= n; i++) {
            nFactorResult = nFactorResult.multiply(BigInteger.valueOf(i));
        }

        int ans = 0;
        while (nFactorResult.mod(BigInteger.TEN).equals(BigInteger.ZERO)) {
            ans++;
            nFactorResult = nFactorResult.divide(BigInteger.TEN);
        }

        return ans;        
    }
}

复杂度分析

• 时间复杂度：\(O(n)\), 实际上应该是 \(O(n + \log n)\)，但 \(\log n\) 很快，只有 \(O(1)\)，所以 \(O(n)\) 。
• 空间复杂度：\(O(1)\)。

方法二：计算1到n中全部5因子数量

思路与算法：

考虑到计算阶乘末尾的每个 \(0\) 表示乘以 \(10\)，那么在我们在计算 \(n!\) 时乘以 \(10\) 的次数是多少？ 考虑到两个数字 \(a\) 和 \(b\) 相乘，例如，要执行 \(15 \times 24 = 360\)，我们可以将其分解为：

\[ 15 \times 24 = 3 \times 5 \times 2 \times 2 \times 2 \times 3 = 360 \]

从上面可以得出，我们只需要考虑 \(2 \times 5\) 的因子有多少对。同时，因为 \(2\) 的因子数比 \(5\) 的因子数要多，所以我们只需要计算 \(1\) 到 \(n\) 的 \(5\) 的因子数有多少即可。