2024 阿里巴巴全球数学竞赛预选赛 试题解答
By Long Luo
阿里巴巴达摩院 从 2018 年开始每年都会举办一届全球数学竞赛,之前一方面自己数学水平比较弱,另外一方面也没有报名,但一直很仰慕那些数学大神的风采。今年是第一次报名参加 2024阿里巴巴全球数学竞赛 ,上周末参加了预选赛,但遗憾的是,全部 \(7\) 道题中只有第 \(1, 2, 6\) 题会做,这里分享下我的解答:
Problem 1
几位同学假期组成一个小组去某市旅游. 该市有 \(6\) 座塔,它们的位置分别为 \(A, B, C, D, E, F\) 。同学们自由行动一段时间后,每位同学都发现,自己在所在的位置只能看到位于 \(A, B, C, D\) 处的四座塔,而看不到位于 \(E\) 和 \(F\) 的塔。已知:
- 同学们的位置和塔的位置均视为同一平面上的点,且这些点彼此不重合;
- 塔中任意 \(3\) 点不共线;
- 看不到塔的唯一可能就是视线被其它的塔所阻挡,例如,如果某位同学所在的位置 \(P\) 和 \(A , B\) 共线,且 \(A\) 在线段 \(PB\) 上,那么该同学就看不到位于 \(B\) 处的塔。
(5 分) 请问 这个旅游小组最多可能有多少名同学?
\(A. 3\)
\(B. 4\) \(C. 6\) \(D. 12\)
Solution
这道题选 \(C\) ,最多只能有 \(6\) 名同学。
这道题的解题思路是从假设只有 \(1\) 座塔开始,一直到 \(6\) 座塔,找到思路。
假设有 \(1\) 座塔 \(A\) ,那么很显然有无数多同学可以看到塔 \(A\) ,也可以有无数多同学看不到塔 \(A\) ;
假设有 \(2\) 座塔 \(A, B\) ,那么只有以 \(A\) 为起点的射线 \(AB\) 且位于 \(B\) 之后的同学无法看到塔 \(A\) ;
假设有 \(3\) 座塔 \(A, B, C\) ,同理可知存在无数位同学至少可以看见 \(2\) 座塔;
假设有 \(4\) 座塔 \(A, B, C, D\) ,同理可知存在无数位同学至少可以看见 \(2\) 座塔;
假设有 \(6\) 座塔 \(A, B, C, D, E, F\) ,如果每位同学都无法看见 \(E, F\) 塔,如下图1 所示:
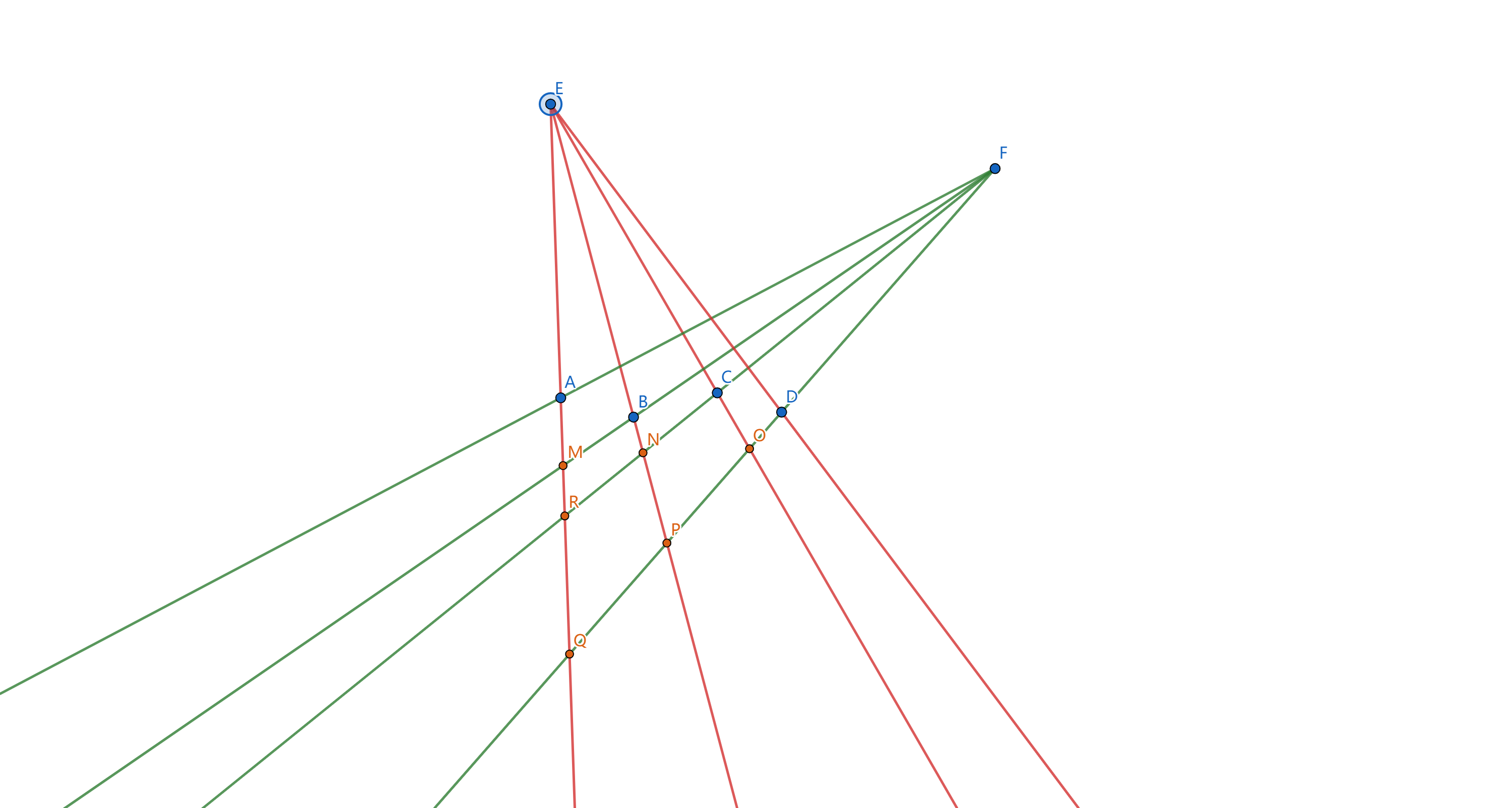
所以至多有 \(6\) 位同学位于 \(M, N, O, P, R, Q\) 处,无法看到塔 \(E, F\) 。