傅里叶变换(Fourier Transform)
By Long Luo
傅里叶变换(Fourier Transform)是什么?
傅里叶变换 1 \((\textit{Fourier Transform})\) 2 和傅里叶级数 \((\textit{Fourier Series})\) 3 是有史以来最伟大的数学发现之一。
傅里叶变换 \((\textit{Fourier Transform})\) 到底是什么,可以看下这个视频 形象展示傅里叶变换 ,讲的非常好。
傅里叶级数和傅里叶变换背后的本质: 任何函数都可以写成正弦函数之和。
如下Gif动图所示: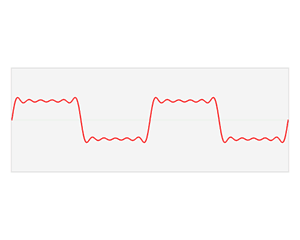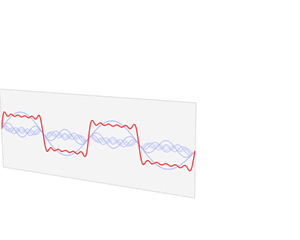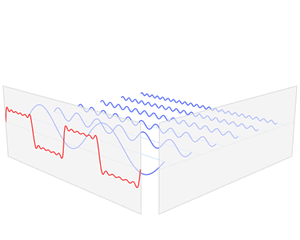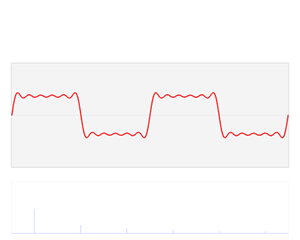
下面这个视频 12分钟的傅立叶级数动画 ,我们可以看到任何图像都可以用大圆套小圆来绘制。
因为我们日常看到的世间万物都会随时间流逝而变化,比如一段声音,一幅图像或者一盏闪烁的交通灯,这种以时间作为参照来观察动态世界的方法我们称其为时域分析。
傅里叶告诉我们任何一个信号都可以用 \(2\) 种方式来表达:
- 时域表达:自变量是时间或者空间的坐标,因变量是信号在该处的强度;
- 频域表达:把信号“展开”成不同频率的简单正弦函数的叠加,相当于看作是定义在所有频率所组成的空间(称为频域空间)上的函数,自变量是不同的频率,因变量是该频率所对应的简谐振动的幅度。
这两个函数一个定义在时域(或空域)上,一个定义在频域上。看起来的样子通常截然不同,但是它们是在以完全不同的方式殊途同归地描述着同一个信号。它们就象是两种不同的语言,乍一听完全不相干,但是其实可以精确地互相翻译。在数学上,这种翻译的过程被称为傅立叶变换\((\textit{Fourier Transform})\) 。
傅里叶变换(Fourier Transform)可以做什么?
在傅立叶变换的所有这些数学性质中,最不寻常的是这样一种特性:一个在时域或空域上看起来很复杂的信号(譬如一段声音或者一幅图像)通常在频域上的表达会很简单。这里「简单」的意思是说作为频域上的函数,它只集中在很小一块区域内,而很大一部分数值都接近于零。例如下图是一张人脸和它对应的傅立叶变换,可以看出,所有的频域信号差不多都分布在中心周围,而大部分周边区域都是黑色的(即零)。
这是一个意味深长的事实,它说明一个在空域中看起来占满全空间的信号,从频域中看起来很可能只不过占用了极小一块区域,而大部分频率是被浪费了的。这就导出了一个极为有用的结论:一个看起来信息量很大的信号,其实可以只用少得多的数据来加以描述。只要对它先做傅立叶变换,然后只记录那些不接近零的频域信息就可以了,这样数据量就可以大大减少。
基本上,这正是今天大多数数据压缩方法的基础思想。在互联网时代,大量的多媒体信息需要在尽量节省带宽和时间的前提下被传输,所以数据压缩从来都是最核心的问题之一。而今天几乎所有流行的数据压缩格式,无论是声音的mp3格式还是图像的jpg格式,都是利用傅立叶变换才得以发明的。从这个意义上说来,几乎全部现代信息社会都建立在傅立叶的理论的基础之上。
关于不确定性原理,可以看下这个讲解的视频:
背景知识
在学习快速傅里叶变换 \((\textit{FFT})\) 之前,有必要先学习一些前置知识,如复数 4,单位复根和多项式。
复数(Complex Number)
复数 \((\textit{Complex Number})\) 是指形如 \(a+bi\) 的数,其中 \(a\) 称为实部 \((\textit{Real part})\), \(b\) 称为虚部 \((\textit{Imaginary part})\) ,\(i\) 为虚数单位,指满足 \(x^2=-1\) 的一个解 \(\sqrt{-1}\) 。复数的集合用 \(\textit{C}\) 表示。
复平面 \((\textit{Complex Plane})\) 是用水平的实轴与垂直的虚轴建立起来的复数的几何表示,复数的实部用沿着 \(\textit{x-axis}\) 的位移表示,虚部用沿着 \(\textit{y-axis}\) 的位移表示。
每一个复数 \(a+bi\) 都唯一对应了一个平面上的向量 \((a, b)\) ,每一个复平面上的向量也唯一对应了一个复数。 \(0\) 既被认为是实数,也被认为是虚数,如下图所示:
复数的模
复数的模是指 \(z\) 在复平面的距离到原点的距离,记作 \(\left| z \right|\) 。
那么对于复数 \(z=a+bi\) ,\(\left| z \right|=\sqrt{a^2+b^2}\) 。
复数的幅角
复数的幅角 \(\theta\) 为实轴的正半轴正方向(逆时针)旋转到 \(z\) 的有向角度,如下图所示:
\[ z = a + bi = \left | r \right | \times ( \cos \theta + i \cdot \sin \theta ) \]
复数的大小
因为虚数 \(i\) 可以理解为逆时针旋转 \(90°\) ,所以虚数无法比较大小。
复数之间的大小关系只存在等于和不等于两种关系,两个复数相等当且仅当实部虚部对应相等。
对于虚部为 \(0\) 的复数之间是可以比较大小的,此时相当于实数之间的比较。
复数的运算
复数之间的运算满足结合律,交换律和分配律。
复数之间的运算法则:
- 加法:满足平行四边形法则。
\[ (a + bi) + (c + di) = (a + c) + (b + d)i \]
- 减法:
\[ (a+bi)-(c+di)=(a-c)+(b-d)i \]
- 乘法:幅角相加,模长相乘。
\[ (a+bi)\cdot(c+di)=ac+adi+bci+bdi^2=(ac-bd)+(ad+cb)i \]
- 除法:
\[ \frac{a+bi}{c+di} = \frac{(a+bi) \cdot (c-di)}{(c+di) \cdot (c-di)} = \frac{(ac+bd)+(bc-ad)i}{c^2+d^2} = \frac{(ac+bd)}{c^2+d^2} + \frac{(bc-ad)i}{c^2+d^2} \]
共轭复数(Complex Conjugate)
对于一个复数 \(z=a+bi\) ,其共轭复数为 \(z^{'}=a-bi\) , \(z^{'}\) 称为 \(z\) 的复共轭 (\(\textit{complex conjugate}\)) 。
共轭复数的性质:
\(z\cdot z^{'}=a^2+b^2\)
\(\left| z \right| = \left| z^{'} \right|\)

单位复根
数学上,数 \(x\) 的 \(n\) 次根 \(r\) 是指: \(r^{n}=x, n=1,2,3,\cdots\) 5。
在复平面上,\(1\) 有 \(n\) 个不同的 \(n\) 次方根,它们位于复平面的单位圆上,构成正多边形的顶点,但最多只可有两个顶点同时标在实数线上。
\(z^{n}=1\) ,该方程复数根 \(z\) 为即为 \(n\) 次单位复根(the \(n\)-th root of unity),如下图所示为 \(1\) 的 \(3\) 个单位复根
将单位圆等分成 \(n\) 个部分,以原点为起点,圆的这 \(n\) 个 \(n\) 等分点为终点,作出 \(n\) 个向量,其中幅角为正且最小的向量称为 \(n\) 次单位向量,记为 \(\omega_{n}^{1}\) 。其余的 \(n-1\) 个向量分别为 \(\omega_{n}^{2},\omega_{n}^{3},......,\omega_{n}^{n}\) ,它们可以由复数之间的乘法得来 \(w_{n}^{k}=w_{n}^{k-1}\cdot w_{n}^{1}\ (2 \leq k \leq n)\) 。
由欧拉公式 \(e^{i\pi}+1=0\) 可知,\(\omega=e^{i\theta}=cos\theta+i \cdot sin\theta\) 。
很容易得出下列公式:
\(\omega_{n}^{n}=\omega_{n}^{0}=1\)
\(\omega_{n}^{k}=e^{\frac{2 \pi k}{n}i}\)。
\(\omega_{n}^{k}=cos(\frac{2 \pi k}{n})+i \cdot sin(\frac{2 \pi k}{n})\)
单位根性质
折半引理
\[ \omega_{2n}^{2k}=\omega_{n}^{k} \]
Proof:
从几何意义来看,两者表示的向量终点是一样的。
\[ \omega_{2n}^{2k}=cos(2\pi\frac{2k}{2n})+i\cdot sin(2\pi\frac{2k}{2n})=cos(2\pi\frac{k}{n})+i\cdot sin(2\pi\frac{k}{n})=\omega_{n}^{k} \]
这条引理可以扩展为:\(\omega_{mn}^{mk}=\omega_{n}^{k}\) 。
消去引理
\[ \omega_{n}^{k+\frac{n}{2}} = -\omega_{n}^{k} \]
Proof:
从几何意义来看,这两者表示的向量终点是相反的,左边较右边在单位圆上多转了半圈。
\[ \omega_{n}^{k + \frac{n}{2}} = cos(2 \pi \frac{k + \frac{n}{2}}{n}) + i \cdot sin(2 \pi \frac{k + \frac{n}{2}}{n}) = cos(2 \pi \frac{k}{n} + \pi) + i \cdot sin(2 \pi \frac{k}{n} + \pi) = -cos(2 \pi \frac{k}{n}) - i \cdot sin(2 \pi \frac{k}{n}) = - \omega_{n}^{k} \]





